さまざまな光学現象を理論で理解しようとすると、なかなか大変。でもとりあえずシミュレーションで様子を見てみると、何だかちょっと分かったような気がするかも…。

シリーズ（1）レンズのコマ収差と絞りによる収差除去
＊参考文献：「光学」久保田 広 著（岩波書店刊）
コマ収差は広義の球面収差の一つです。屈折面に対して斜めに主光線が入射する場合に発生する収差で、1点から出た光が1点に集光せず一方に尾を曳いてしまう、なかなか厄介な現象です。このコマ収差の様子と、それを除去する方法の一例をシミュレーションソフトで見てみることにしましょう。

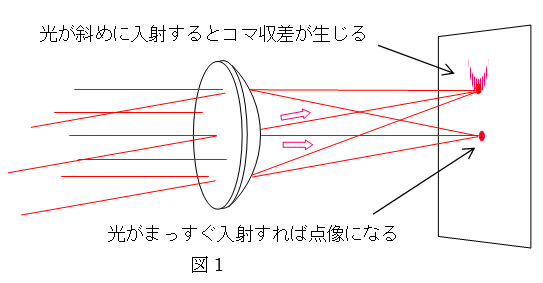
『　コマ収差のない場合としては、次の3つがあります。一つの屈折面について、
ⅰ) 物体が曲率中心にあるとき
ⅱ）物体が不遊点にあるとき
ⅲ）絞りが曲率中心にあるとき
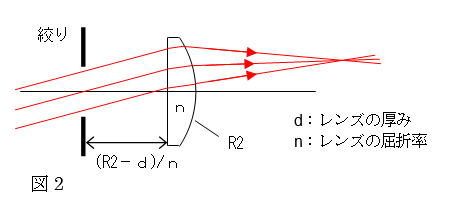
平凸レンズの場合、次の2つの条件を満たすとこのⅰ)とⅲ）に合致し、コマ収差を除去することができます。
①光源（物点）が無限遠にある（平行光が入射する）。
②絞りが、第2面（球面）の曲率中心の第1面による像の所にある。

＊以上、上記「光学」10-4レンズのコマ収差　より抽出　』
この絞りの効果を、シミュレーションソフト「ZEMAX®」を使って見てみることにしましょう。
尚、絞りを入れてもその位置が②の条件を満たさなければ、見掛け上は集光像が小さくなっても、コマ収差自体は無くならないことも合わせて見て行きましょう。

シミュレーション条件は以下のようにしました。
○波　長　　：550nm、光源の大きさは0mm（点光源）
○光線入射角：15°
○平凸レンズ：石英製φ25、f50、fb46.00、Ct5.84(→d)、r22.92(→R2)　
○絞りの位置：レンズ前11.70mm〔計算式は図2から（R2－d）／n＝（22.92－5.84）／1.460＝11.70〕

まず、このレンズの基本的な集光状態をシミュレーションで見ておきます。絞りは開放です。
１．レンズの基本的な集光状態のシミュレーション
主光線がレンズの軸に一致しているときの集光像です。

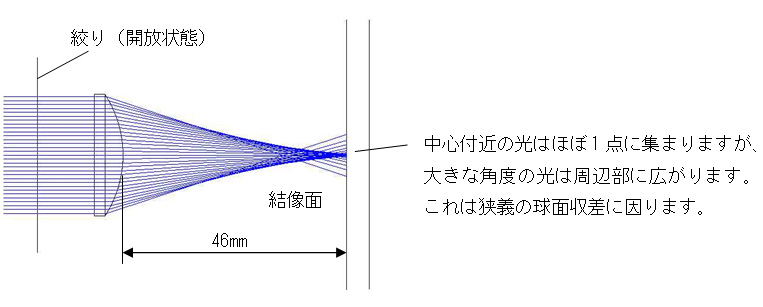
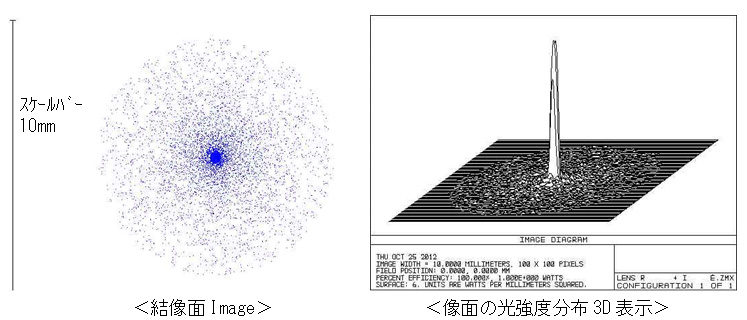光は中心に集中していますが、周辺にも薄く広がっていまる様子が分かります。

中心部はおよそφ0.4mm程度に集光しています。周辺部に薄く広がるのは、狭義の球面収差（レンズの中心から離れた位置に入射した光の焦点距離が短くなります）のためです。
以下、狭義の球面収差を「球面収差」と記します。

続いて光を斜め15°で入射させ、発生するコマ収差をシミュレーションで見てみます。

２．コマ収差のシミュレーション
＊絞りはありません。

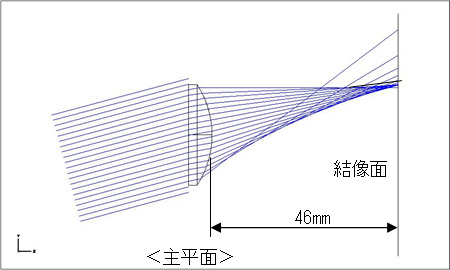
光が片側に（非対称的に）広がっています。

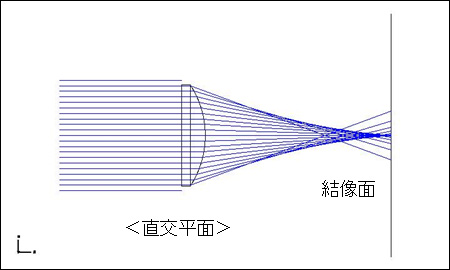
上図と直交する方向から見ると光は両側に（対称的に）広がっています。

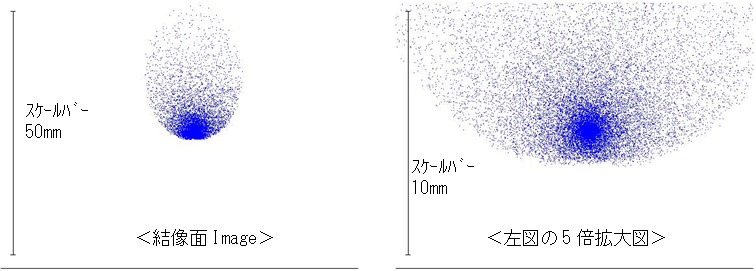
像は中心から上方に薄く広がった形状になっています。

上図のように、光像は中心から一方向へ広く薄く広がることが示されました。これがコマ収差と言われる現象です。

次に、絞りを計算値（P2参照）の位置に入れた状態で集光像がどうなるかを見てみましょう。
２．絞りを入れた状態のシミュレ－ション（絞りの大きさとコマ収差の変化を見ていきます。）
①絞りの直径φ25（レンズの直径と同じ）の場合

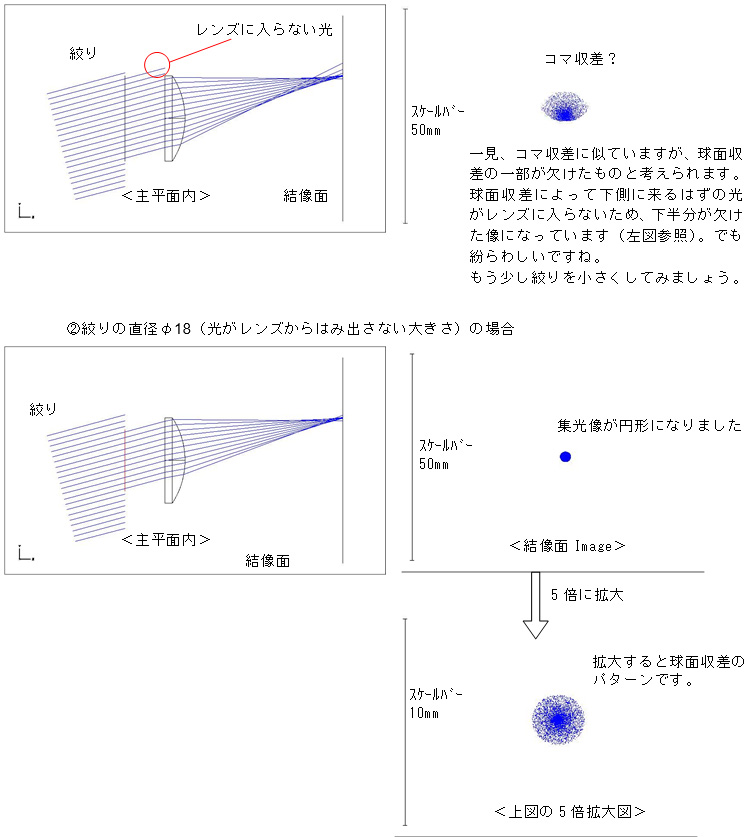
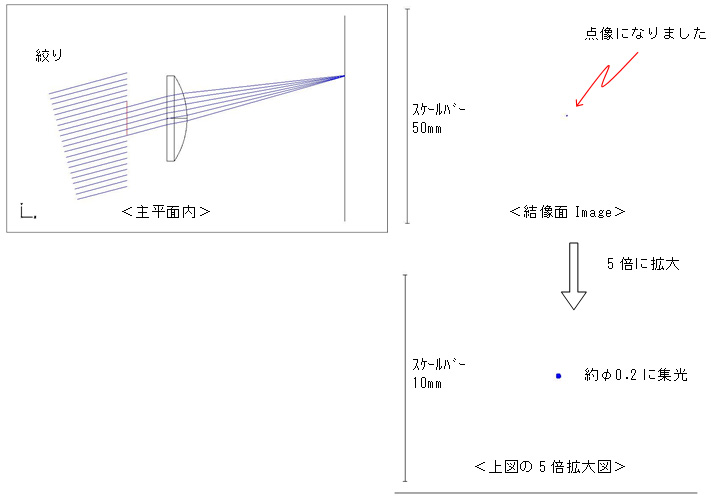
このようにシミュレーションをしてみると、絞りを適正な位置に設置するとコマ収差が消えることが分かりました。ただ、絞りの開口が大き過ぎて光の一部がレンズ面からはみ出す場合には、集光像の一部が欠けて、コマ収差に似た形になることも示され、開口の大きさも重要であることが分かりました。更に絞りを小さくすると（この例ではφ10）結像状態が格段に改善されました。これは、残っていた球面収差が小さくなったためと考えられます。

理論的に示されたコマ収差(*)を除去する絞りの働きの一例が、このシミュレーションでも確認できました。
なんだか少し分かったような気がしませんか？

では最後に、あえて適正ではない位置に絞りを入れたらどうなるか、を見てみましょう。
適正な位置は（P2参照）レンズの前方11.70mm〔＝(R2－d)／n〕ですが、ここでは、試しにレンズの前方1.0mmに入れてみます。

①絞りの直径φ18（適正な位置では結像が円形になった条件）の場合
光の一部が上方に広がっています。

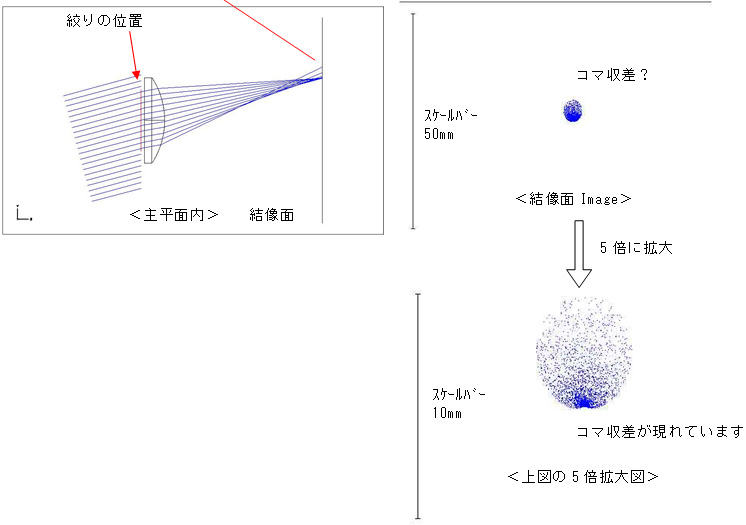
コマ収差がはっきり現れました。

②絞りの直径φ10（適正な位置では光が点像になった条件）の場合

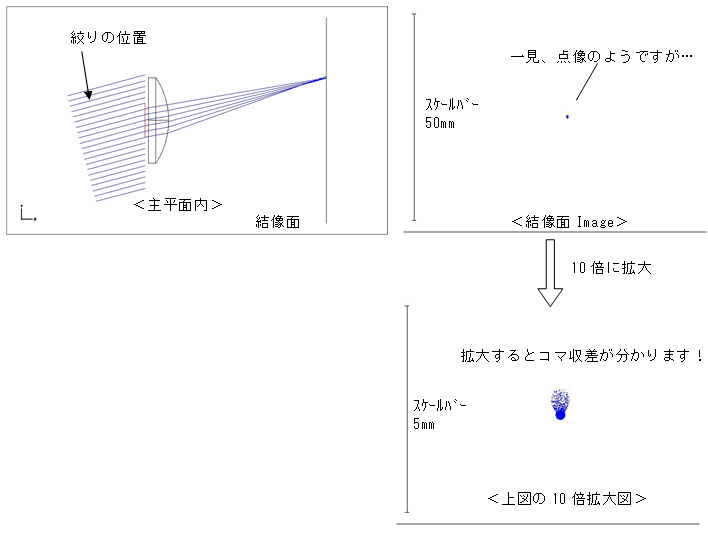
絞りをここまで絞っても、コマ収差は残りました。
「絞り」をいくら絞ってもその位置が適正でないと、光が球面と対称性がもてないため、やはりコマ収差が現れると云うことのようですね。
もう一度、なんだ少し分かったような気がしませんか？

本当かな？シミュレーション Part2